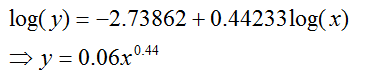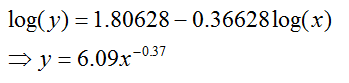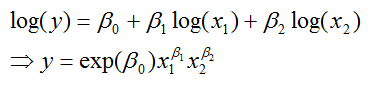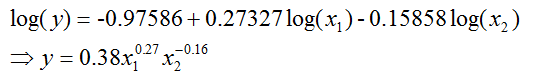Statistical Consultants Ltd

HomeServicesBlogLinksAboutContact


ICT Development Index 2010


Data Tables, Statistical Modelling, Information Technology, Economics

Date posted: 23 March 2012


The International Telecommunication Union (ITU) is a United Nations agency responsible for information and communication technology (ICT).  The ITU have published several ICT related indices, including an ICT Development Index (IDI) and an ICT Price Basket (IPB) for most countries.
 
The IDI is a composite of 11 indicators, and is used to compare the overall level of ICT development between countries.  The IDI has three sub-indices based on ICT access, use and skills.  

The IPB is a composite basket based on the prices for fixed telephone, mobile cell-phone, and fixed broadband internet services, expressed as a percentage of average income levels.

The indices were first published by the ITU in 2009, using 2008 data.  At the time of writing, the most recent versions were published in 2011, and based on 2010 data.
 

ICT Development Index (IDI) by Country


Country IDI 2010 Rank IDI 2010 IDI 2008 Rank IDI 2008
Korea (Rep.)  1 8.40 1 7.80
Sweden  2 8.23 2 7.53
Iceland  3 8.06 7 7.12
Denmark  4 7.97 3 7.46
Finland  5 7.87 12 6.92
Hong Kong, China  6 7.79 6 7.14
Luxembourg  7 7.78 4 7.34
Switzerland  8 7.67 9 7.06
Netherlands  9 7.61 5 7.30
United Kingdom  10 7.60 10 7.03
Norway  11 7.60 8 7.12
New Zealand  12 7.43 16 6.65
Japan  13 7.42 11 7.01
Australia  14 7.36 14 6.78
Germany  15 7.27 13 6.87
Austria  16 7.17 21 6.41
United States  17 7.09 17 6.55
France  18 7.09 18 6.48
Singapore  19 7.08 15 6.71
Israel  20 6.87 23 6.20
Macao, China  21 6.84 27 5.84
Belgium  22 6.83 22 6.31
Ireland  23 6.78 19 6.43
Slovenia  24 6.75 24 6.19
Spain  25 6.73 25 6.18
Canada  26 6.69 20 6.42
Portugal  27 6.64 29 5.70
Italy  28 6.57 26 6.10
Malta  29 6.43 31 5.68
Greece  30 6.28 30 5.70
Croatia  31 6.21 36 5.43
United Arab Emirates  32 6.19 32 5.63
Estonia  33 6.16 28 5.81
Hungary  34 6.04 34 5.47
Lithuania  35 6.04 35 5.44
Cyprus  36 5.98 43 5.02
Czech Republic  37 5.97 37 5.42
Poland  38 5.95 41 5.29
Slovak Republic  39 5.94 40 5.30
Latvia  40 5.90 39 5.31
Barbados  41 5.83 33 5.47
Antigua & Barbuda  42 5.63 38 5.32
Brunei Darussalam  43 5.61 44 4.97
Qatar  44 5.60 48 4.50
Bahrain  45 5.57 42 5.16
Saudi Arabia  46 5.42 55 4.13
Russia  47 5.38 49 4.42
Romania  48 5.20 46 4.67
Bulgaria  49 5.19 45 4.75
Serbia  50 5.11 47 4.51
Montenegro  51 5.03 50 4.29
Belarus 52 5.01 58 3.93
TFYR Macedonia  53 4.98 52 4.20
Uruguay  54 4.93 51 4.21
Chile  55 4.65 54 4.14
Argentina  56 4.64 53 4.16
Moldova  57 4.47 64 3.57
Malaysia  58 4.45 57 3.96
Turkey  59 4.42 60 3.81
Oman  60 4.38 68 3.45
Trinidad & Tobago  61 4.36 56 3.99
Ukraine  62 4.34 59 3.83
Bosnia and Herzegovina  63 4.31 63 3.58
Brazil  64 4.22 62 3.72
Venezuela  65 4.11 61 3.73
Panama  66 4.09 67 3.52
Maldives  67 4.05 66 3.54
Kazakhstan  68 4.02 72 3.39
Mauritius  69 4.00 70 3.43
Costa Rica  70 3.99 69 3.45
Seychelles  71 3.94 65 3.56
Armenia  72 3.87 86 2.94
Jordan  73 3.83 73 3.29
Azerbaijan  74 3.78 83 2.97
Mexico  75 3.75 74 3.26
Colombia  76 3.75 71 3.39
Georgia  77 3.65 85 2.96
Albania  78 3.61 81 2.99
Lebanon  79 3.57 77 3.12
China  80 3.55 75 3.17
Viet Nam  81 3.53 91 2.76
Suriname  82 3.52 78 3.09
Peru  83 3.52 76 3.12
Tunisia  84 3.43 82 2.98
Jamaica  85 3.41 79 3.06
Mongolia  86 3.41 87 2.90
Iran (I.R.)  87 3.39 84 2.96
Ecuador  88 3.37 88 2.87
Thailand  89 3.30 80 3.03
Morocco  90 3.29 100 2.60
Egypt  91 3.28 92 2.73
Philippines  92 3.22 95 2.69
Dominican Rep.  93 3.21 89 2.84
Fiji  94 3.16 90 2.82
Guyana  95 3.08 93 2.73
Syria  96 3.05 96 2.66
South Africa  97 3.00 94 2.71
El Salvador  98 2.89 101 2.57
Paraguay  99 2.87 97 2.66
Kyrgyzstan  100 2.84 99 2.62
Indonesia  101 2.83 107 2.39
Bolivia  102 2.83 102 2.54
Algeria  103 2.82 105 2.41
Cape Verde  104 2.81 103 2.50
Sri Lanka  105 2.79 106 2.41
Honduras  106 2.72 104 2.42
Cuba  107 2.69 98 2.62
Guatemala  108 2.65 108 2.39
Botswana  109 2.59 109 2.25
Uzbekistan  110 2.55 110 2.22
Turkmenistan  111 2.50 111 2.15
Gabon  112 2.42 112 2.10
Namibia  113 2.36 114 2.06
Nicaragua  114 2.31 113 2.09
Kenya  115 2.29 116 1.74
India  116 2.01 117 1.72
Cambodia  117 1.99 120 1.63
Swaziland  118 1.93 115 1.80
Bhutan  119 1.93 123 1.58
Ghana  120 1.90 118 1.68
Lao P.D.R.  121 1.90 119 1.64
Nigeria  122 1.85 125 1.54
Pakistan  123 1.83 121 1.59
Zimbabwe  124 1.81 128 1.49
Senegal  125 1.78 129 1.46
Gambia  126 1.74 122 1.59
Yemen  127 1.72 127 1.49
Comoros  128 1.67 130 1.44
Djibouti  129 1.66 124 1.56
Côte d'Ivoire  130 1.61 132 1.43
Mauritania  131 1.58 126 1.50
Angola  132 1.58 136 1.31
Togo  133 1.57 134 1.36
Nepal  134 1.56 137 1.28
Benin  135 1.54 138 1.27
Cameroon  136 1.53 133 1.40
Bangladesh  137 1.52 135 1.31
Tanzania  138 1.51 141 1.23
Zambia  139 1.50 131 1.44
Uganda  140 1.49 140 1.24
Madagascar  141 1.45 142 1.20
Rwanda  142 1.44 143 1.18
Papua New Guinea  143 1.38 139 1.24
Guinea  144 1.31 144 1.16
Mozambique  145 1.30 146 1.10
Mali  146 1.26 145 1.11
Congo (Dem. Rep.)  147 1.17 147 1.04
Eritrea  148 1.09 148 1.03
Burkina Faso  149 1.08 149 0.98
Ethiopia  150 1.08 150 0.94
Niger  151 0.92 152 0.79
Chad  152 0.83 151 0.80


IDI versus GDP per capita (PPP)


ICT Development Index (IDI) vs GDP per capita (PPP) graph


IDI increases at a decreasing rate with respect to GDP per capita (PPP).  The GDP per capita (PPP) figures were from the World Bank, mostly from 2010 (with a few from earlier years).  A regression model was fitted to quantify this relationship.


Regression model output:


Call:
lm(formula = log(IDI2010) ~ log(GDPpcppp2010))
 
Residuals:
     Min       1Q   Median       3Q      Max
-0.65459 -0.09432  0.02275  0.13098  0.68191
 
Coefficients:
                  Estimate Std. Error t value Pr(>|t|)   
(Intercept)       -2.73862    0.12613  -21.71   <2e-16 ***
log(GDPpcppp2010)  0.44233    0.01383   31.98   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.2092 on 148 degrees of freedom
  (2 observations deleted due to missingness)
Multiple R-squared: 0.8735,     Adjusted R-squared: 0.8727
F-statistic:  1022 on 1 and 148 DF,  p-value: < 2.2e-16



For those who aren’t familiar with regression output:


The high (close to one) R-squared statistic shows that the model fits strongly to the data:
 
Multiple R-squared: 0.8735


The very low (close to zero) p-values, show that the parameters of the model are highly significant:

Pr(>|t|)   
<2e-16 ***
<2e-16 ***


These figures are the coefficient estimates, used to construct the model. 

                  Estimate
(Intercept)       -2.73862
log(GDPpcppp2010)  0.44233


The fitted model is represented by the following equation:

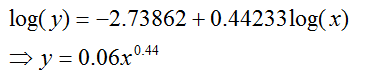
IDI vs GDP per capita regression model equation

Where:
   x is GDP per capita (PPP)
   y is the IDI


The fitted regression model curve added to the plot:

ICT Development Index (IDI) vs GDP per capita graph with regression model curve


The two variables are interdependent i.e. they both depend on each other rather than one being dependent and the other being independent.  As GDP per capita (PPP) increases, on average the more affordable the development of information and communication technology becomes.  Investing in information and communication technology can result in higher GDP per capita (PPP), due to higher productivity, lower costs of production, and the development of high-tech industries.


IDI versus IPB


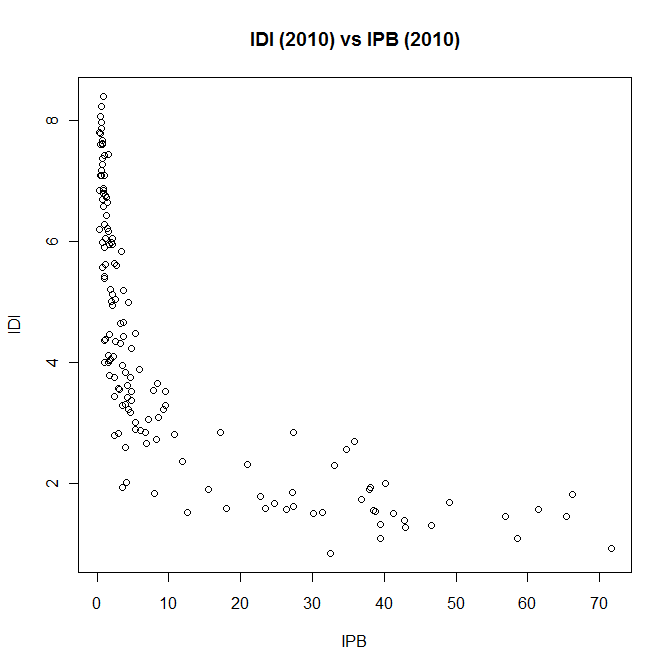
ICT Development Index (IDI) vs ICT Price Basket (IPB) graph


IDI decreases at a decreasing rate with respect to IPB.  A regression model was fitted to quantify this relationship.
 
 
Regression model output:


Call:
lm(formula = log(IDI2010) ~ log(ICTpricebasket2010))
 
Residuals:
     Min       1Q   Median       3Q      Max
-0.71750 -0.12492  0.02376  0.15908  0.49380
 
Coefficients:
                        Estimate Std. Error t value Pr(>|t|)   
(Intercept)              1.80628    0.02599   69.50   <2e-16 ***
log(ICTpricebasket2010) -0.36628    0.01267  -28.92   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.2221 on 143 degrees of freedom
  (7 observations deleted due to missingness)
Multiple R-squared: 0.854,      Adjusted R-squared: 0.8529
F-statistic: 836.2 on 1 and 143 DF,  p-value: < 2.2e-16



For those who aren’t familiar with regression output:


The high (close to one) R-squared statistic shows that the model fits strongly to the data:
 
Multiple R-squared: 0.854


The very low (close to zero) p-values, show that the parameters of the model are highly significant:

Pr(>|t|)   
<2e-16 ***
<2e-16 ***


These figures are the coefficient estimates, used to construct the model. 

                  Estimate
(Intercept)        1.80628
log(GDPpcppp2010) -0.36628


The fitted model is represented by the following equation:

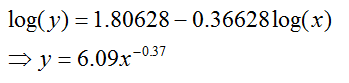
IDI vs IPB regression model equation

Where:
   x is the IPB
   y is the IDI


The fitted regression model curve added to the plot:

ICT Development Index (IDI) vs ICT Price Basket (IPB) graph with regression model curve


The two variables are interdependent.  The lower the price of information and communication technologies (relative to income), the more affordable it is to adopt those technologies, resulting in a higher quantity of demand for them (resulting in a higher IDI).  The development of information and communication technology infrastructure results in an increase in supply, resulting in lower prices for information and communication technologies.


IDI Combined Model


A regression model was constructed which includes both IPB and GDP per capita (PPP).
 
The model has the following structure:

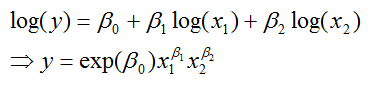
Structure of the combined model

where:
   y is the IDI
   x1 is GDP per capita (PPP)
   x2 is the IPB


Regression model output:

Call:
lm(formula = log(IDI2010) ~ log(GDPpcppp2010) + log(ICTpricebasket2010))
 
Residuals:
     Min       1Q   Median       3Q      Max
-0.63013 -0.11554  0.01074  0.12034  0.54496
 
Coefficients:
                        Estimate Std. Error t value Pr(>|t|)   
(Intercept)             -0.97586    0.38346  -2.545   0.0120 * 
log(GDPpcppp2010)        0.27327    0.03755   7.277 2.23e-11 ***
log(ICTpricebasket2010) -0.15858    0.03139  -5.052 1.34e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.1862 on 140 degrees of freedom
  (9 observations deleted due to missingness)
Multiple R-squared: 0.8984,     Adjusted R-squared: 0.8969
F-statistic: 618.7 on 2 and 140 DF,  p-value: < 2.2e-16


The fitted model is represented by the following equation:

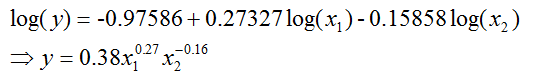
Combined model (fitted)

where:
   y is the IDI
   x1 is GDP per capita (PPP)
   x2 is the IPB


The combined model is similar to the constant price elasticity demand model used in econometrics.  A constant price elasticity demand model would have the logged quantity (or logged expenditure) explained by the logged price and other variables that explain demand, including a variable related to income.  The coefficient of the logged price explanatory variable is interpreted as the price elasticity of demand i.e. a 1% increase in price, would result in a percentage change in the quantity demanded on average equal to the coefficient estimate.


Download the Data Set

 
The data set containing the IDI, IPB and GDP per capita (PPP) data can be downloaded here.

Note that:
  • If a country doesn’t have an IDI figure but did have an IPB figure, they weren’t included in the data set. 
  • Some countries don’t have IPB values.
  • There were more missing IPB values for 2008 than for 2010.
  • There are missing values in the GDP per capita (PPP) data.
  • Some of the GDP per capita (PPP) figures are from before 2010.


External link:

ITU Measuring the Information Society


See also:

Regression

HomeServicesBlogLinksAboutContact

Copyright © Statistical Consultants Ltd  2012