Statistical Consultants Ltd

Prosecutor's Fallacy

Justice, Ethics, Law, Probability

Prosecutor’s fallacies (with respect to statistics) are fallacies of statistical reasoning that can result and have resulted in miscarriages of justice.

The fallacy usually involves the jury being presented with an incorrectly calculated probability and/or a probability that they are conned into believing is the probability the defendant is innocent.

Example – The Sally Clark Case

Sally Clark was a British solicitor who was wrongly convicted of the murder of two of her sons.

Her first son died suddenly within a few weeks of birth in 1996. After her second son died in a similar manner, she was arrested in 1998 and then tried for the murder of both sons.

Professor Sir Roy Meadow, a paediatrician, presented faulty statistical evidence against her. He said that the chance of two children from a wealthy family suffering sudden infant death syndrome (SIDS) was 1 in 73 million. He calculated this figure by squaring 1/8500; his estimate of the likelihood of a single cot death occurring in similar circumstances.

The Royal Statistical Society later issued a public statement expressing its concern at the ‘misuse of statistics in the courts’ and argued that Meadow’s claim had ‘no statistical basis’.

Meadow’s statistical reasoning was severely flawed for the following reasons:

Incorrectly calculated marginal probabilities
The 1 in 8500 figure was estimated inaccurately. The probability of a child dying from SIDS would be closer to 1 in 3000. Meadow came to his figure by taking into account factors that made SIDS less likely for that case, but ignored other factors that greatly increase the likelihood of SIDS such as the fact that the children were boys.

Conditional probabilities were ignored
The two children would have been genetically similar and would have been living in a similar environment. Although the cause of SIDS is yet unknown, it is highly plausible that genetic and environmental factors would affect the likelihood of its occurrence. In 2004, an article written by Mathematics Professor Ray Hill and published in Paediatric and Perinatal Epidemiology, concluded (using extensive SIDS statistics for England) that ‘after a first cot death the chances of a second become greatly increased’, by a dependency factor of between 5 and 10.

Joint probability misinterpreted as the probability of innocence
Even if the 1 in 73 million figure was valid, it wouldn’t be the probability of innocence. To estimate the probability of innocence, the jury would have needed to weigh up the relative likelihood of the two competing explanations for the children’s deaths i.e. SIDS and murder. Although double SIDS is very rare, double infant murder is even rarer, therefore the probability that Clark was innocent would have been quite high.

Sally Clark was convicted in 1999. The convictions were eventually overturned in 2003 after it emerged that the prosecutor’s pathologist had failed to disclose microbiological reports suggesting that one of her sons had died of natural causes. As a result of the case, the Attorney-General ordered a review of hundreds of other cases, which lead to two other women having their convictions of murdering their children overturned.

Multiple Comparisons

Sometimes the fallacy is due to not correcting for multiple comparisons. This problem can happen when DNA profiling is used.

For example, let’s say that a crime scene DNA sample is compared against a database of 20,000 men. The DNA sample matches the profile of one of the men, and that man is accused of the crime. At the trial it is stated that the probability of two DNA profiles matching by chance is only 1 in 10,000. This is not the probability of innocence, yet some juries could easily be conned into thinking it was.

Since 20,000 men were tested, there were 20,000 opportunities to find a match by chance.

Even if no one in the database left the crime scene 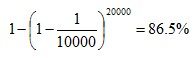DNA, a match by chance to an innocent man is more likely than not. The probability of getting at least one match by chance would be:

Calculation

The larger the database, the more likely it is for there to be a match by chance alone.

Balance of Probabilities vs. Proving Guilt

Some people reading this might be thinking ‘if the probability of innocence could be accurately calculated, and if guilt was more likely than innocence, the defendant should be convicted’. This line of thinking is severely flawed, very dangerous, and unfortunately quite common.

Many would deem it far worse to punish an innocent man for a crime he didn’t commit, than to let a criminal go unpunished. If the courts were to treat both scenarios as equally bad (and take a balance of probabilities), then everyone in society would have far more reason to fear being severely punished for something they may or may not have done. If the courts were to only find people guilty if there was absolute certainty of guilt, then only criminals would have reason to fear being punished.

Unfortunately absolute certainty is rare and the concept of reasonable doubt comes into play. Despite attempts at maintaining innocence until proven guilty, there have been numerous accounts of miscarriages of justice. In some cases, the defendant is innocent but the level of doubt about them being guilty is deemed unreasonable at the time of trial. The defendant might later be found not guilty (or even proven innocent), based on things such as:

Evidence discovered after the trial (possibly from new forensic technology)
A more thorough analysis of the original evidence
A change in the level of doubt deemed reasonable

In statistical hypothesis testing, the significance level is analogous to the level of reasonable doubt in a trial.