Statistical Consultants Ltd |
      |
Social Welfare FunctionsEconomics, Mathematics Utility is a term used by economists to describe the level of an individual's satisfaction, especially from the consumption of goods and services. There are various theoretical measures of a society’s collective utility i.e. its social welfare. Various social welfare functions (SWF) have been suggested, that are functions of a society’s individual level utilities. UtilitarianOne of the utilitarian measures of a society’s welfare is the sum of all individual utilities:  Where: W
is the society’s
welfare (collective utility)
Ui is the utility of individual i N is the total number of people in society Alternatively, the utilitarian measure could instead take the average (mean) utility rather than the total.  RawlsianThe Rawlsian measure of society’s welfare equals the utility of the individual who is worst off.  Bernoulli-NashThe Bernoulli-Nash SWF goes some way to find a mix of the utilitarian and Rawlsian SWFs. Bernoulli-Nash SWF (total): 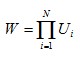 Bernoulli-Nash SWF (average): 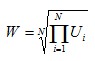 Note that this average is the geometric mean utility. Iso-elasticIt is possible to take a more generalised mix of the utilitarian and Rawlsian welfare functions. One way is to use an iso-elastic welfare function:  Where a is a constant and is greater than or equal to zero. If a = 0, the SWF is utilitarian (total) As a approaches 1, the SWF becomes Bernoulli-Nash (total) As a approaches ∞, the SWF becomes Rawlsian Graphing SWFs with indifference curvesThe social welfare functions described above can be graphed using indifference curves. Each point on an indifference curve represents an equal amount of welfare. The further the curve is from the origin, the higher the level of welfare. For a two person society, the indifference curves for the SWFs would look like the following:    See also:Utility Functions |
      |
| Copyright © Statistical Consultants Ltd 2010 |